Karmaşık veri çözümlemesi yapmak için Çözümleyici Araç Takımı'nı kullanma
Veri çözümleme işlevleri, herhangi bir zamanda, yalnızca bir çalışma sayfasında kullanılabilir. Veri çözümlemeyi, gruplandırılan çalışma sayfalarında uyguladığınızda, sonuçlar ilk çalışma sayfasında görünür ve kalan çalışma sayfalarında boş, biçimlenmiş tablolar görünür. Kalan çalışma sayfalarında veri çözümleme uygulamak için, çözümleme aracını, her bir çalışma sayfası için yeniden hesaplayın.
Çözümleyici Araç Takımı aşağıdaki bölümlerde açıklanan araçları içerir. Bu araçlara erişmek için Veri sekmesinin Çözümlemegrubunda Veri Çözümleme'yi tıklatın. Veri Çözümleme komutu kullanılamıyorsa, Çözümleyici Araç Takımı eklenti programını yüklemeniz gerekir.
Çözümleyici Araç Takımı'nı yükleme ve etkinleştirme
-
Dosya sekmesini tıklatın, Seçenekler'i ve sonra da Eklentiler kategorisini tıklatın.
-
Yönet kutusunda Excel Eklentileri'ni seçin ve ardından Git'i tıklatın.
-
Eklentiler kutusunda, Çözümleyici Araç Takımı onay kutusunu işaretleyin ve sonra da Tamam' ı tıklatın.
-
Çözümleyici Araç Takımı, Kullanılabilir eklentiler kutusunda listelenmiyorsa, yerini belirtmek için Gözat'ı tıklatın.
-
Çözümleyici Araç Takımı'nın şu anda bilgisayarınızda yüklü olmadığı uyarısı geldiğinde, yüklemek için Evet seçeneğini tıklatın.
-
Ne öğrenmek istiyorsunuz?
Anova
Anova çözümleme araçları farklı türden varyans çözümlemelerine imkan verir. Kullanmanız gereken araç, sınamak istediğiniz veri gruplarından aldığınız etmen sayısına ve örnek sayısına bağlıdır.
Anova: Tek Etmen
Bu araç, iki veya daha çok örnek için verilerde basit bir varyans çözümlemesi yapar. Bu çözümleme, temel olasılık dağılımlarının tüm örnekler için aynı olmadığı yönündeki alternatif varsayıma karşılık, her örneğin aynı temel olasılık dağılımından alındığı varsayımının sınanmasını sağlar. Yalnızca iki örnek varsa, çalışma sayfası işlevi T.TEST kullanılabilir. İkiden fazla örnek olduğunda,T.TEST için uygun bir genelleme yoktur ve bunun yerine Tek Etmenli Anova modelinden yararlanılabilir.
Anova: Yinelemeli Çift Etmen
Bu çözümleme aracı, veriler iki farklı boyut üzerinde sınıflandırılabildiğinde yararlıdır. Örneğin, bitkilerin yüksekliğini ölçme deneyinde, bitkilere farklı markalarda gübre (örneğin, A, B, C) verilebilir ve ayrıca farklı sıcaklıklarda tutulabilir (örneğin, yüksek, düşük). Altı olası çiftin {gübre, sıcaklık} her biri için, eşit sayıda bitki uzunluğu gözlemimiz vardır. Bu Anova aracını kullanarak şunu sınayabiliriz:
-
Farklı gübre markaları için bitki uzunluklarının aynı temel popülasyondan ileri gelip gelmediği. Bu çözümleme için sıcaklıklar yoksayılır.
-
Farklı sıcaklık düzeyleri için bitki uzunluklarının aynı temel popülasyondan ileri gelip gelmediği. Bu çözümleme için gübre markaları yoksayılır.
Tüm çift (gübre, sıcaklık) değerlerinin aynı popülasyondan ileri geldiğini temsil eden altı örnekte, ilk madde işaretli noktada bulunan gübre markaları ile ikinci madde işaretli noktada bulunan sıcaklıklar arasındaki farkların etkilerinin hesaba katılıp katılmadığını. Alternatif varsayım, tek başına gübre veya tek başına sıcaklığa dayalı belirli çiftlerin (gübre, sıcaklık) üstündeki farklar nedeniyle oluşan etkilerin varlığıdır.
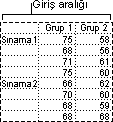
Anova: Yinelemesiz Çift Etmen
Bu çözümleme aracı, Yinelemeli Çift Etmen durumunda olduğu gibi veriler iki farklı boyut üzerinde sınıflandırılabildiğinde yararlıdır. Ancak, bu araç için her çift (örneğin, yukarıdaki örnekteki her çift {gübre, sıcaklık}) için yalnızca tek bir gözlem olduğu varsayılır.
Korelasyon
CORREL ve PEARSON çalışma sayfası işlevlerinin her ikisi de, her bir değişkendeki ölçümler N konularının her biri için gözlendiğinde iki ölçüm değişkeni arasındaki korelasyon katsayısını hesaplar. (Herhangi bir konu için herhangi bir kayıp gözlem, konunun çözümlemede yok sayılmasına neden olur.) Korelasyon çözümleme aracı, N konularının her biri için ikiden daha fazla ölçüm değişkeni olması durumunda özellikle yararlıdır. Bu, ölçüm değişkenlerinin olası her bir çiftine uygulanan CORREL (veyaPEARSON) değerini gösteren bir çıkış tablosu, bir korelasyon matrisi sağlar.
Kovaryans gibi korelasyon katsayısı, "birlikte değişen" iki ölçüm değişkenine genişletilmesinin bir ölçümüdür. Kovaryanstan farklı olarak, korelasyon katsayısı iki ölçüm değişkeninin ifade edildiği birimlerin bağımsız değeri olacak şekilde ölçeklendirilir. (Örneğin, iki ölçüm değişkeni ağırlık ve yükseklik olursa, ağırlık pound biriminden kilogram birimine çevrildiğinde korelasyon katsayısı değeri değişmez.) Herhangi bir korelasyon katsayısının değeri -1 ile +1 arasında olmalıdır.
Korelasyon çözümlemesi aracını, birlikte hareket eğilimi olan iki ölçüm değişkenini belirlemek için her bir ölçüm değişkeni çiftini incelemek amacıyla , diğer bir deyişle, bir değişkenin büyük değerlerinin, diğer değişkenin büyük değerleriyle ilişkili olma eğiliminin olup olmadığını [pozitif korelasyon], bir değişkenin küçük değerlerinin, diğer değişkenin büyük değerleriyle ilişkili olma eğiliminin olup olmadığını [negatif korelasyon] veya her iki değişken değerlerin ilişkisiz olma eğiliminde olup olmadığını [0'a (sıfır) yakın korelasyon] belirlemek için) kullanabilirsiniz.
Kovaryans
Korelasyon ve Kovaryans araçlarının ikisi de, bireyler kümesinde gözlenen farklı N ölçüm değişkenleriniz olduğunda aynı ayarda kullanılabilir. Korelasyon ve Kovaryans araçlarının her biri, ölçüm değişkenlerinin her biri arasında sırasıyla korelasyon katsayısını veya kovaryansı gösteren bir çıkış tablosu, bir matris verir. Fark, korelasyon katsayılarının -1 ile +1 (dahil) arasında olacak şekilde ölçeklendirilmeleridir. Karşılık gelen kovaryanslar ölçeklendirilmezler. Korelasyon katsayısı ve kovaryansın her ikisi "birlikte değişen" iki ölçüm değişkenine genişletilmesinin bir ölçümüdür.
Kovaryans aracı, her bir ölçüm değişkeni çifti için çalışma sayfası işlevi KOVARYANS.P'ın değerini hesaplar. (Kovaryans aracının aksine KOVARYANS.P'nin doğrudan kullanımı, yalnızca iki ölçüm değişkeninin olması durumunda (N=2) akla yakın diğer bir seçenektir.) Kovaryans aracının çıkış tablosunun i satırı, i sütunu köşegenindeki giriş, i-nci ölçüm değişkeninin kendisiyle kovaryansıdır. Bu, o değişken için çalışma sayfası işlevi VAR.P tarafından hesaplandığı gibi sadece popülasyon değişkenidir.
Kovaryans aracını, birlikte hareket etme eğilimi olan iki ölçüm değişkenini belirlemek için her bir ölçüm değişkeni çiftini incelemek amacıyla , diğer bir deyişle, bir değişkenin büyük değerlerinin, diğer değişkenin büyük değerleriyle ilişkili olma eğiliminin olup olmadığını [pozitif kovaryans], bir değişkenin küçük değerlerinin, diğer değişkenin büyük değerleriyle ilişkili olma eğiliminin olup olmadığını [negatif kovaryans] veya her iki değişken değerlerin ilişkisiz olma eğiliminde olup olmadığını [0'a (sıfır) yakın kovaryans] belirlemek için) kullanabilirsiniz.
Tanımlayıcı İstatistik
Tanımlayıcı İstatistik çözümleme aracı, giriş aralığındaki verilerin tek değişkenli istatistiğinin bir raporunu oluşturarak verilerinizin merkezi eğilimi ve çeşitliliği hakkında bilgi verir.
Üstel Düzeltme
Üstel Düzeltme çözümleme aracı, önceki tahmindeki hatayı düzeltip, önceki dönem tahmini esasında değeri tahmin eder. Araç, büyütülmüş hali tahminlerin önceki tahmindeki hatalara ne kadar güçlü yanıt verildiğini belirleyen a düzeltme sabitini kullanır.
NOT : 0,2 ile 0,3 arasındaki değerler, düzeltme sabitleridir. Bu değerler, geçerli tahminin, önceki tahmindeki hatanın yüzde 20 ile yüzde 30'una ayarlanması gerektiğini belirtir. Daha büyük sabitler, daha hızlı yanıt verir; fakat hatalı tahminler oluşturabilir. Daha küçük sabitler, tahmin değerleri için uzun gecikmelere neden olabilir.
F Sınaması: Varyanslar İçin İki Örnek
F Sınaması: Varyanslar İçin İki Örnek çözümleme aracı iki popülasyonun varyansını karşılaştırmak için iki örnekli F sınaması gerçekleştirir.
Örneğin, F Sınamasını, bir yüzme karşılaşması sonuçlarının, iki takımdan alınan zaman örnekleri üzerinde kullanabilirsiniz. Araç, temel alınan dağılımda eşit olmayan değişkenler için diğer bir seçeneğe karşı eşit değişkenlerle olan dağılımlardan gelen bu iki örneğin boş varsayım sınamasının sonucunu sağlar.
Araç, bir F istatistik değerinin (veya F oranı) f değerini hesaplar. 1'e yakın olan bir f değeri, temel alınan popülasyon değerlerinin eşit olduğuna dair kanıt sağlar. Çıkış tablosunda, popülasyon varyanslarının eşit olması durumunda, f < 1 ise “P(F <= f) tek kuyruklu” denklemi F istatistik değerinin gözlenme olasılığının f'den az, “F Kritik tek kuyruklu” denklemi ise, seçilen Alpha önem düzeyi için 1'den küçük kritik değer verir. F > 1 ise, “P(F <= f) tek kuyruklu” denklemi F istatistik değerinin gözlenme olasılığının f'den çok, “F Kritik tek kuyruklu” denklemi ise Alpha için 1'den büyük kritik değer verir.
Fourier Çözümlemesi
Fourier Çözümlemesi aracı, doğrusal sistemlerdeki problemleri çözer ve periyodik verileri, verileri dönüştürmek için Fast Fourier Transform (FFT) yöntemi kullanarak çözümler. Bu araç aynı zamanda, dönüştürülen verilerin başlangıçtaki verilere döndürüldüğü ters dönüşümleri de destekler.
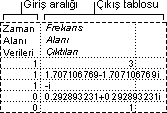
Histogram
Histogram çözümleme aracı, bir veri ve veri kümesi hücre aralığı için, tek tek ve kümülatif sıklıkları hesaplar. Bu araç, bir değerin, bir veri kümesindeki olay sayısı için, veri oluşturur.
Örneğin, 20 öğrenciden oluşan bir sınıfta, harf notu kategorilerinde, derecelerin dağılımını belirleyebilirsiniz. Bir histogram tablosu, harf notu sınırlarını ve en düşük sınırla geçerli sınır arasındaki derece sayısını sunar. Tek, en sık görülen derece verilerin modudur.
İPUCU : Excel 2016'da çubuk grafik veya Pareto grafiği artık oluşturabilirsiniz.
Hareketli Ortalama
Hareketli Ortalama çözümleme aracı, tahmin dönemindeki değerleri, değişkenin belirli sayıdaki önceki dönemlerdeki ortalama değerine dayanarak planlar. Bir hareketli ortalama, tüm tarihsel verilerin basit bir ortalamasının maskeleyeceği eğilim bilgileri sağlar. Bu aracı, satışları, envanteri ve diğer eğilimleri tahmin etmek için kullanın. Tahmin değerlerinin tümü aşağıdaki formüle dayanır.
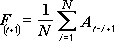
burada:
-
N, hareketli ortalamaya katılacak önceki dönem sayısıdır.
-
A j, j zamanındaki gerçek değerdir.
-
F j, j zamanındaki tahmin edilen değerdir.
Rasgele Sayı Üretimi
Rasgele Sayı Üretimi çözümleme aracı, bir aralığı, birçok dağılımdan alınabilen bağımsız rastgele sayılarla doldurur. Bir popülasyondaki özneleri, bir olasılık dağılımıyla gösterebilirsiniz. Örneğin, bireylerin boylarından oluşan popülasyonu göstermek için normal dağılım kullanabilirsiniz veya para atma sonuçları popülasyonunu göstermek için, Bernoulli dağılımının iki olası sonucunu kullanabilirsiniz.
Derece ve Yüzdebirlik
Derece ve Yüzdebirlik çözümleme aracı, bir veri kümesindeki her bir değerin sıra ve yüzde sıralı konumunu içeren bir tablo oluşturur. Bir veri tablosundaki değerlerin göreceli durumunu çözümleyebilirsiniz. Bu araç RANK.EŞİT ve YÜZDERANK.DHLçalışma sayfası işlevlerini kullanır. Bağlı değerleri hesaba katmak isterseniz, bağlı değerlerle aynı sıraya sahipmiş gibi işlem yapanRANK.EŞİT işlevini kullanın veya bağlı değerler için ortalama sırayı getiren RANK.ORT işlevini kullanın.
Regresyon
Regresyon çözümleme aracı, bir satırı bir gözlem kümesinin içine uydurmak için, "en küçük kareler" yöntemi kullanarak doğrusal regresyon uygular. Tek bağımsız değişkenin bir veya birden çok bağımsız değişkenin değerinden nasıl etkilendiğini çözümleyebilirsiniz. Örneğin, bir atletin performansının yaş, boy ve ağırlık gibi etmenlerden nasıl etkilendiğinin çözümlemesini yapabilirsiniz. Performans ölçümlerindeki payları, bir performans verileri kümesini esas alarak bu üç etmenden her birine paylaştırabilir; sonra da bu aldığınız sonuçları yeni ve sınanmamış bir atletin performansını tahmin etmekte kullanabilirsiniz.
Regresyon aracı, çalışma sayfası işlevi LINEST'i kullanır.
Örnekleme
Örnekleme çözümleme aracı, giriş aralığını bir popülasyon olarak düşünerek, bir popülasyondan bir örnek oluşturur. Popülasyon, işlemek veya çizimini oluşturmak için çok büyük olduğunda, tanıtıcı bir örnek kullanabilirsiniz. Giriş verilerinin periyodik olduğunu düşünüyorsanız, bir çevrimin yalnızca belirli bir bölümündeki değerleri içeren bir örnek de oluşturabilirsiniz. Örneğin, giriş aralığı, üç aylık satış rakamlarını içeriyorsa, giriş aralığındaki aynı üç aydan dört yerli değerlerin periyodik bir oranıyla örnekleme.
t Sınaması
İki Örnek t Sınaması çözümleme araçları, her bir örneği temel alan popülasyon ortalamalarının eşitliğini sınar. Bu üç araç üç farklı varsayım kullanır; popülasyon değişkenlerinin eşit olması, popülasyon değişkenlerinin eşit olmaması ve iki örneğin aynı konu üzerinde işlemden önceki ve işlemden sonraki gözlemleri temsil etmesi.
Aşağıdaki üç aracın tümü, hesaplanan bir t, t-İstatistik değerdir ve çıkış tablolarında “t Stat” olarak gösterilir. Verilere bağlı olarak, bu değer, t, negatif veya negatif olmayan bir değer olabilir. Popülasyon ortalamalarının eşitliğini temel alan varsayım altında, t < 0, “P(T <= t) tek kuyruklu” t-İstatistik değerinin t'den daha fazla negatif olduğunun gözlenebileceği olasılığını verir. t >=0, “P(T <= t) tek kuyruklu” ise t-İstatistik değerinin t'den daha pozitif olduğunun gözlenebileceği olasılığını verir. “t Kritik tek kuyruklu” kesme biçimi değerini verir, böylece t-İstatistik değerinin "t Kritik tek kuyruklu"dan büyük veya eşit olduğunun gözlenme olasılığının Alpha olduğunu verir.
“P(T <= t) iki kuyruklu” t-İstatistik değerinin mutlak değerde t'den daha büyük olduğunun gözlenebileceği olasılığını verir. “P Kritik iki kuyruklu” kesme biçimi değerini verir, böylece mutlak değerde gözlenen t-İstatistik değerinin “P Kritik iki kuyruklu”'dan daha büyük Alpha olma olasılığını verir.
t Sınaması: Ortalamalar için Eşli İki Örnek
Eşli sınamayı örneklerde, bir örnek grubunun deneyden önce ve sonra olmak üzere iki kez sınanması durumunda olduğu gibi doğal eşleşmenin olduğu durumlarda kullanabilirsiniz. Bu çözümleme aracı ve onun formülü, iki örnekli bir Öğrenci t Sınamasını, bir işlemden önce alınan gözlemler ve bir işlemden sonra alınan gözlemlerin büyük bir olasılıkla eşit popülasyon ortalamalı dağılımlardan gelmiş olup olmadıklarını belirlemek için uygular. Bu t Sınaması formu her iki popülasyonun da eşit olduğunu varsaymaz.
NOT : Bu araçlar tarafından oluşturulan sonuçlar arasında, aşağıdaki formülden türetilen, verilerin ortalama etrafındaki dağılımının birikimli bir ölçüsü olan birikimli varyans da yer alır.
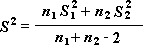
t Sınaması: Varyansları Eşit Kabul Edilen İki Örnek
Bu çözümleme aracı, iki örnekli bir öğrenci t Sınaması uygular. Bu t Sınaması biçimi her iki veri kümesinin aynı değişkenlerle olan dağılımından geldiğini varsayar. Buna, homoscedastic t Sınaması denir. Bu t Sınamasını, iki örneğin büyük bir olasılıkla eşit popülasyon ortalamalarıyla gelmiş olup olmadığını belirlemek için kullanabilirsiniz.
t Sınaması: Varyansları Eşit Kabul Edilmeyen İki Örnek
Bu çözümleme aracı, iki örnekli bir öğrenci t Sınaması uygular. Bu t Sınaması formu, her iki veri kümesinin eşit olmayan varyanslı dağılımlardan geldiğini varsayar. Buna, heteroscedastic t sınaması denir. Yukarıdaki Eşit Varyanslar durumunda olduğu gibi, bu t Sınamasını, iki örneğin büyük bir olasılıkla eşit popülasyon ortalamalı dağılımlardan gelmiş olup olmadığını belirlemek için kullanabilirsiniz. Bu sınamayı, iki örnekte ayrı konular olması durumunda kullanın. Tek bir konular kümesi ve işlemden önce ve sonra her bir konu için ölçümleri temsil eden iki örnek olması durumunda, aşağıdaki örnekte tanımlanan, Çiftli sınamayı kullanın.
Aşağıdaki formül, istatistik değeri t'yi saptamak için kullanılır.
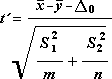
Aşağıdaki formül serbestlik derecelerini, df, hesaplamak için kullanılır. Çünkü hesaplamanın sonucu genellikle tamsayı değildir, t tablosundan kritik bir değer elde etmek için df değeri en yakın tamsayıya yuvarlatılır. Excel çalışma sayfası işlevi T.TEST, hesaplanan df değerini yuvarlatmadan kullanır, çünkü T.TEST için tamsayı olmayan bir değerle hesap yapmak olasıdır. Serbestlik derecelerini belirlemedeki bu farklı yaklaşımlardan dolayı, T.TEST sonuçları ve bu t Sınaması aracı Eşit Olmayan Varyanslar durumunda farklılık yaratacaktır.
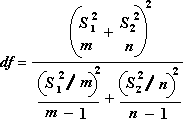
z Sınaması
z Sınaması: Ortalamalar İçin İki Örnek çözümleme aracı bilinen varyanslı ortalamalar için, iki örnekli bir z Sınaması uygular. Bu araç, tek yanlı ya da iki yanlı farklı varsayım seçeneklerine karşı iki popülasyon ortalaması arasında fark olmayan boş varsayımı sınamakta kullanılır. Eğer varyanslar bilinmiyorsa onun yerine çalışma sayfası işlevi Z.TEST kullanılmalıdır.
z Sınaması aracını kullanırken, çıkışı anlamak için dikkatli olun. “P(Z <= z) tek kuyruklu” P(Z >= ABS(z)'ye eşittir), popülasyon ortalamalarıyla arasında bir fark olmadığı durumda gözlenen z değeri gibi aynı yönde bir z değerinin 0'dan uzak olma olasılığıdır. “P(Z <= z) iki kuyruklu” P(Z >= ABS(z) veya Z <= -ABS(z)'ye eşittir), popülasyon ortalamaları arasında hiç fark olmadığı durumda bir z değerinin gözlenen z değerinden farklı yönde 0'dan uzak olma olasılığıdır. İki kuyruklu sonuç, tek kuyruklu sonucun yalnızca 2 ile çarpılmasıdır. z Sınaması aracı ayrıca, iki popülasyon ortalamaları arasındaki fark için belirli bir sıfır olmayan değer boş varsayımı olması durumunda da kullanılabilir. Örneğin, bu sınamayı, iki araba modelinin performansı arasındaki farkları belirlemek için kullanabilirsiniz.
Çözümleme Araç Takımı için VBA işlevleri
Çözümleme Araç Paketine Visual Basic for Application (VBA) işlevlerini de eklemek için, ToolPak Çözümleyicisi VBA Eklentisini, ToolPak Çözümleyicisiyle aynı şekilde yükleyebilirsiniz. Kullanılabilir eklentiler kutusunda, ToolPak - VBA Çözümleyicisi onay kutusunu işaretleyin.